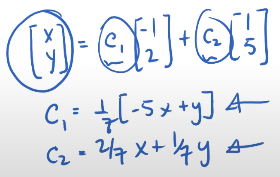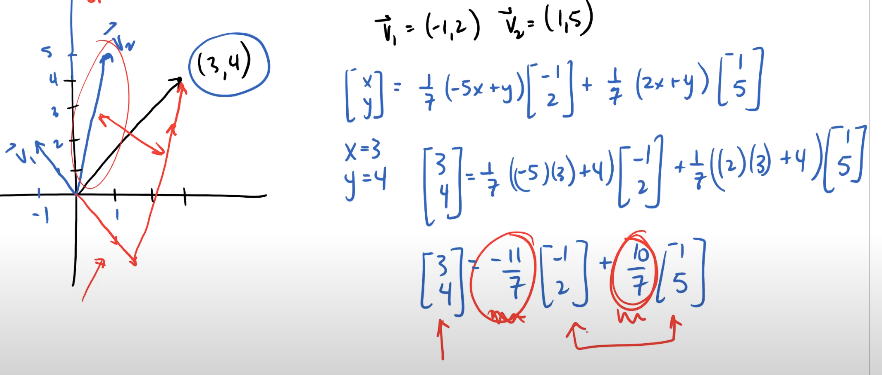Status: Tags: #cards/math232/unit1 Links: Vectors
Basis
Principles
?
- Set of vectors ($v_1$, $v_2$, $v_3$) in $R^2$, $R^3$ is a basis if
- span{$v_1$, $v_2$, $v_3$} = $R^2$, $R^3$ and
- {$v_1$, $v_2$, $v_3$} is linearly independent
- Allows you to get to any point with the set of vectors
Prove that the set {(−1, 2),(1, 5)} is a basis for R2 ?
- Check on whether it is possible to find any point using a combination of x and y by solving for c1 and c2
-
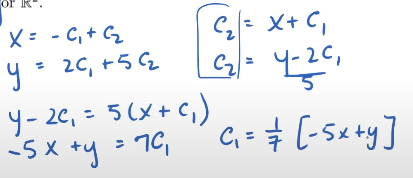
- Thus, its now possible to find any point so it is $R^2$
- Linear independence since (-1,2) cannot be multiplied by any k to equal (1,5)
- Used as a basis to get to point (3,4)
Standard Basis
- (1,0), (0,1) for $R^2$
- For matrices with more than 1 row, iterate through the matrix like a double for loop, i=row and j=column
Examples
Find basis of range of linear mapping
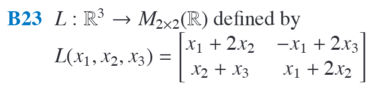 ?
?
- Create n matrices multiplied by $c_n$ where n is subscript of x, put respective coefficients
- ex) c1[1 -1 ; 0 1] + c2[] + c3[]
- Remove any that are linearly dependent
Backlinks
References:
Created:: 2022-01-11 20:38