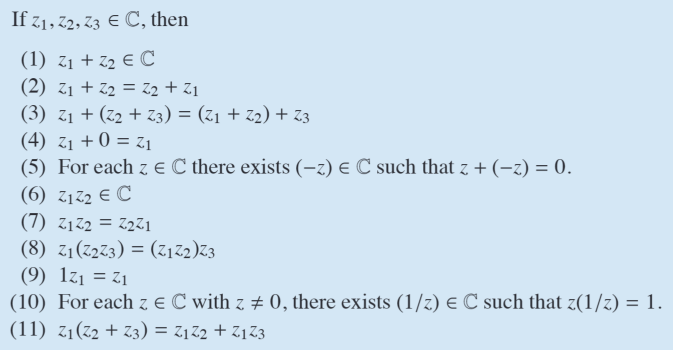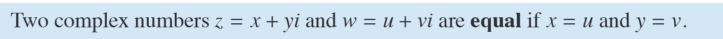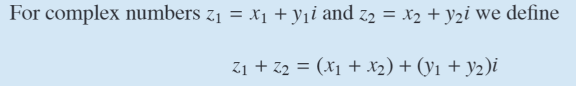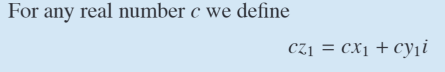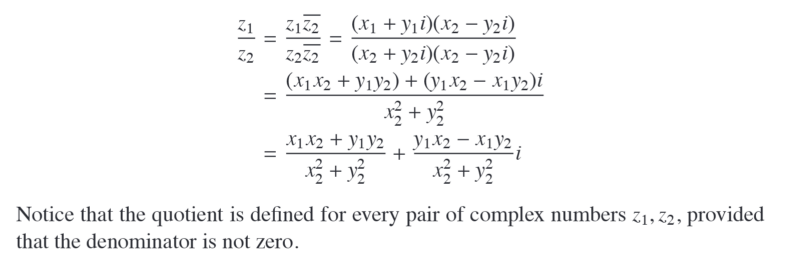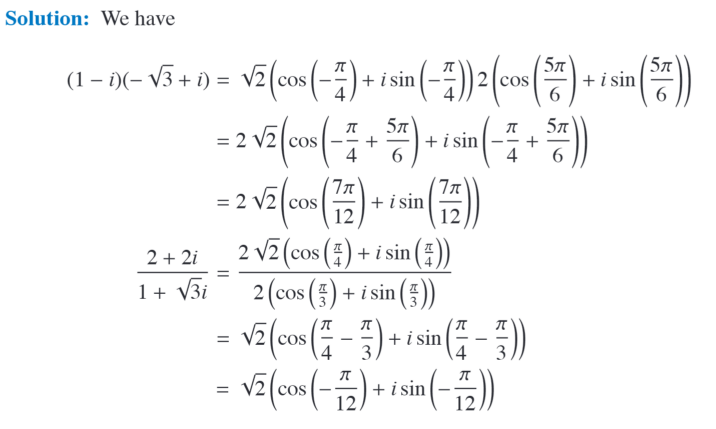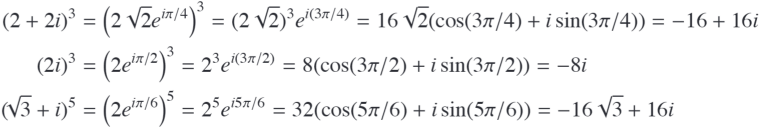Status: Tags: #cards/math232/unit9 Links: Number Theory
Complex Numbers
Principles
?
- ^ Standard form
- Has real part $Re(z) = x$ and imaginary part $Im(z) = yi$
- If y != 0, then z = yi is purely imaginary
- x + iy is used for polar coordinates
- Can be represented algebraically, graphically, and as Polar Forms
Uses
- Finding n-th Roots
Properties
?
Argument of z
?
- Every complex number has infinite arguments, but usually the principal argument (wihtin -pi < theta < pi) is chosen
- if theta is an arg of a comp num z, then all values $theta + 2k(pi), k (- Z$, are also arguments of Z
modulus of a product is ;; the product of the moduli of the factors
argument of a product is ;; the sum of the arguments
Bar above equation implies ;; absolute value
The i when finding the length ;; disappears
i*i = ;; -1
Complex Exponentials
de Moivre’s Formula $z=r(cos\theta+isin\theta)$ with r!=0, then for any integer n we have ?
- $z^n=r^n(cosn\theta+isinn\theta)$
Definitions
$\frac{1}{w} = ?$ ? $\frac{\bar{w}}{{|w|}^2}$
Equality
?
Modulus (absolute value of a complex number)
?
Complex conjugate
?
- Reflection over x axis
- Properties
-
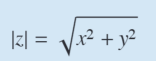
Operations
Addition
Scalar multiplication
Multiplication
?
Quotient of two complex numbers
?
- Multiply both numerator and denominator by complex conjugate of denominator, simplify
-
Complex numbers in $R^2$
?
- Any complex number z is a point (x,y) in $R^2$
- x-axis is real axis, and y-axis is imaginary
- xy plane is the complex plane
Diagram of complex numbers in $R^2$
?
- Diagram called Agrand diagram
Examples
Find all arguments of z = 1-i
?
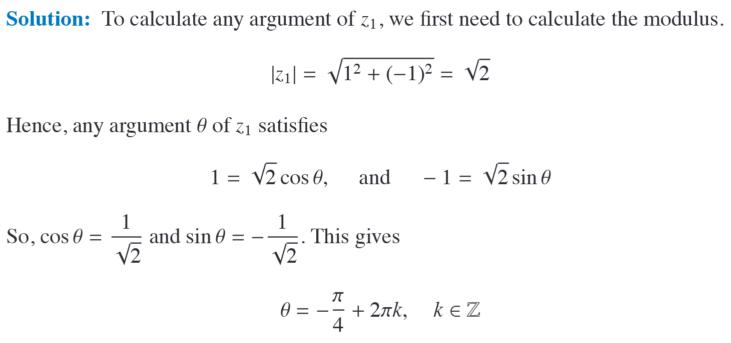
Determine principle argument of $\sqrt{3} + i$
?
?
?
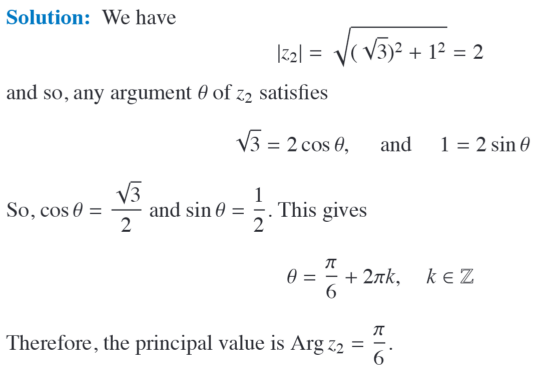
References:
Created:: 2022-03-07 18:04