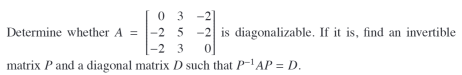Status: Tags: #cards/math232/unit6 Links: Matrix
Diagonalization
Principles
Similar Matrices ?
- When $P^{-1}AP = B$ for some invertible matrix $P$ ** Trace of A ?
- tr(A) = $a_{11}$ + $a_{22}$ + … + $a_{nn}$
If A,B (- R such that $P^{-1}AP = B$ for some invertible matrix $P$, then $A$ and $B$ have the same ?
- Determinant
- Eigenvalues
- Rank
- Trace
Theorems
A matrix is diagonalizable iff every eigenvalue of the matrix has ?
- geo mult = alg mult
If A (- R has n distinct eigenvalues, then ;; A is diagonalizable
Diagonalization Theorem
?
- Square matrix A is only diagonalizable iff a basis for $R^n$ exists that consists of eigenvectors of $A$
Examples
References:
Created:: 2022-03-14 04:31