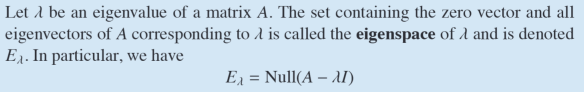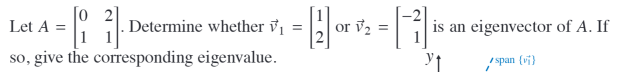Last updated April 10, 2022

Status: Tags: #cards/math232/unit6 Links: Vectors

Eigenvalues and Eigenvectors

• Eigenvectors of Linear Mappings

Principles

Eigenvalue and Eigenvector ?

• Special vector of matrix that is mapped by the matrix to a scalar multiple of itself
• 
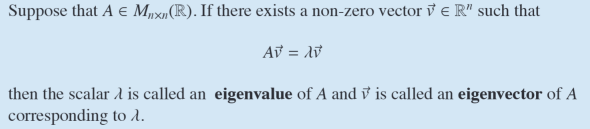
• eigenvector should be non-zero
• Each eigenvector of A will lead to an eigenvalue, but each eigenvalue will have infinitely many eigenvectors

Characteristic polynomial ?

• C(λ) = det(A-λI)
• Highest degree has coefficient $(-1)^n$

Dominant Eigenvalue

Dominant eigenvalue ?

• The eigenvalue larger than the rest

Power method for approximating eigenvalues ?

• Choose random vector (do [1,1]) and find right value through eqn
• then keep multiplying matrix with newfound vector until you see a pattern and deduce the eigenvector
• Do matrix multiplication with A and deduced eigenvector, then GCF out the number $c$ to have $c\vec{v}$
  • $c$ is dominant eigenvalue

Algebraic and Geometric Multiplicity

Algebraic multiplicity ?

• alg mult of λ is number of times λ is repeated as a root of the characteristic polynomial
  • Literally just degree of the root

Geometric multiplicity ?

• geo mult is dimension of eigenspace of λ
  • The number of vectors in the nullspace basis

Relationship between alg and geo mult ?

• 1 <= geo mult <= alg mult

geo < alg implies that the eigenvalue is ;; deficient

if for all eigenvalues, geo mult = alg mult, then ?

• sums will equal each other which equal n
• if we collect all basis vectors from eigenspaces, we will end up with n vectors in $R^n$
  • linear independent, form as basis for $R^n$

A is invertible implies that ?

• λ is not an eigenvalue of A

Finding Eigenvalues of a Matrix A

?

• refer to pg. 350 / 367
• There must be v1,v2 != 0 such that A[v1,v2] = λ[v1,v2]
• Can be turned into linear systems, turn into standard form (=0)
• Only eigenvalue if non-zero solutions provide a non-zero vector v
  • Use Matrix Inverse / use determinant to see when determinant = 0
    • ad-bc, find root of polynomial

Finding infinite eigenvectors of eigenmatrix

?

• Find solution space of homogeneous system with coefficient matrix
• Nullspace of $(A-λ)\vec{v}$
• Only add λ to a and d, then RREF

Eigenspace

?

• Minimum 1 dimension

Examples

?

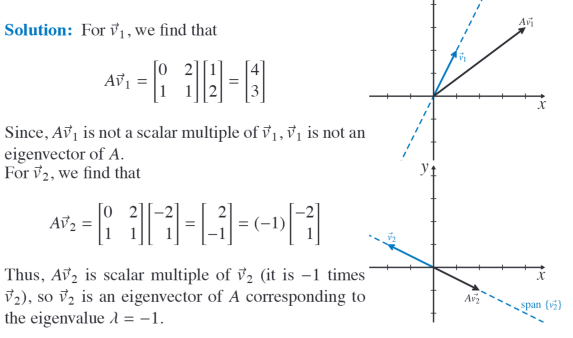
Find eigenvalues and vectors of the matrix A = $\begin{bmatrix} 17 & -15 \20 & -18 \end{bmatrix}$ ?

References:

Created:: 2022-03-09 16:25