Last updated April 10, 2022

Status: Tags: #archivedCards/macm101/numbertheory Links: Division

Greatest Common Divisor

Principles

• Denoted by gcd(a,b)

For integers a and b, a positive integer c is said to be a common divisor of a and b if ?

• c | a and c | b
• For any common divisor d of a and b, we have d | c

Prove greatest comon divisor always exists, For any positive integers a and b, there is a unique positive integer c such that c is the greatest common divisor of a and b ?

• Set notation is multiples of all divisors of a,b

• Finally, if c and d are greatest common divisors, then c | d and d | c. Thus c = d.

Theorem

Proof: If a, b are integers and d is their greatest common divisor, then there are integers u, v such that d = au + bv. ?

• Keep using previous definitions to climb back to the top

Examples

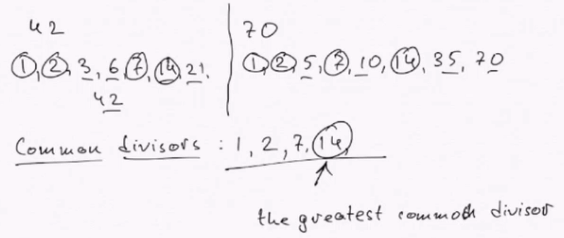
Greatest common divisor of 42 and 70? ?

Euclidean Algorithm

• Euclidean Algorithm Find greatest common divisor of 821 and 123 ?
• Continue using division algorithm to find a smaller comparison for gcd

Backlinks

1

list from Greatest Common Divisor AND !outgoing(Greatest Common Divisor)

References:

Created:: 2021-11-25 16:32