Last updated April 10, 2022

Status: Tags: #cards/math232/unit2 Links: System of linear equations

Homogeneous linear system

Principles

?

• When each of its equations are homogeneous
  • Last column of augmented matrix consist of only zeros
  • $b_i$ = 0 where b is the LHS

Solutions of a homogeneous linear system ?

• Always has one solution, trivial solution when $x_i$ = 0 for all i
  • nontrivial solutions
• If there is one nontrivial solution, then there are infinite since applying a scalar to LHS will still equal 0
• Therefore, either only trivial or infinite solutions
  • 

• Solution of a homogeneous is based on free variables
  • If there are some, isolate x1 and represent them as the free variables
  • If there are none, then solution is empty vector

Solution Space

?

• Is a subspace, called solution space
• Since homo always has 0 as solution set, we can’t just test it
• Closed under scalar mult due to homogeneous nature
• Closed under vector addition

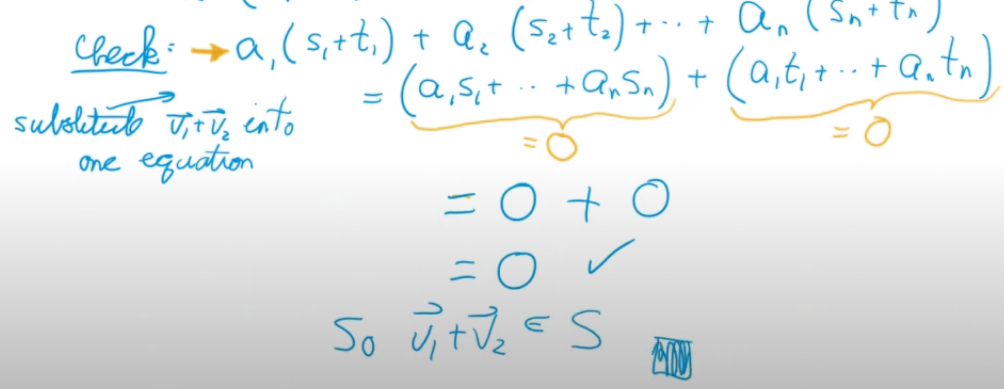
To find solution/basis, move free variables to RHS and find the vector equation

Dimensions is number of free variables

Questions

Find a homogeneous system that defines the given subspace

• 2.3 B4-11 ?
• RREF, back substitution

Backlinks

1

list from Homogeneous linear system AND !outgoing(Homogeneous linear system)

References:

Created:: 2022-01-22 13:59