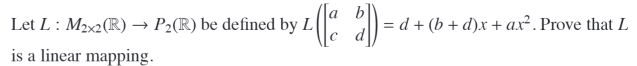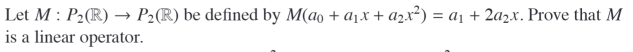Last updated April 10, 2022

Status: Tags: #cards/math232/unit3 #cards/math232/unit4 Links: Vector Line Equations

Linear Mapping

Principles

? Ø = some transformation $R^n$ → $R^n$

• Ø(kx) = kØ(x)
  • linear with respect to scalar product
• Ø(x+y) = Ø(x) + Ø(y)
  • linear wrt vector addition

Linear operators ?

• Linear mappings but dimensions stay the same

Checking if a vector is in a range of a linear mapping ?

• Create liner system with x components = y components
• RREF
• In range if consistent, RHS is the x vector such that L(x) = y

Types

Zero mapping as a linear operator ?

• Z(v) = 0w for all v in V

Identity mapping as a linear operator ?

• Maps to itself

Nullsp

Checking

Check if you can turn Ø(tx+sy) = tØ(x) + sØ(y)

• Apply t, s, etc to the preimage, then substitute those expanded components into the image
• Need to find form tL($\vec{x}$) + sL($\vec{y}$)

Rules

• For any linear mapping, Ø, Ø(0 vector) = 0
  • since k=0 would set everything to 0
• No constant terms/homogeneous
• No exponents
• Mapping is linear iff it is a matrix mapping

Examples

Determine if the following mappings are linear and express them as a matrix mapping ?

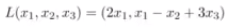• Ø(tx+sy) => tØ(x) + sØ(y) where t and s are just generic scalars
• work towards that general solution
• first step is scalar multiplication
• next is vector addition, end up with the different components
• apply the transformation onto the respective components
• expand
• gcf t and s, factor out the equation and you’re left with the LHS

?

• L(s(x) + t(y)) = sL(x) + tL(y)
• Distribute s and t, combine into one matrix
• Plug into image
• GCF s, end up with the image ?

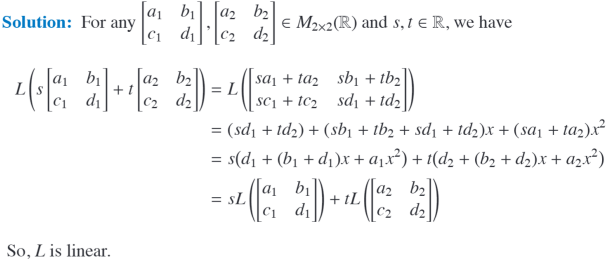
Backlinks

1

list from Linear Mapping AND !outgoing(Linear Mapping)

References:

Created:: 2022-01-28 21:06