Status: Tags: #cards/math232/unit7 Links: Orthogonal - Basis
Orthogonal Bases
Maybe revisit orthogonal matrix/orthonormal basis notes (pg. 405)
Principles
?
- If for any $v_i$ and $v_j$ where i != j, $v_i (v_j) = 0$
- Satisfies pythagorean theorem
Linear dependence of orthogonal bases ?
- Linearly independent since its never 0 vector so length cannot equal 0, meaning $c_1$ != 0
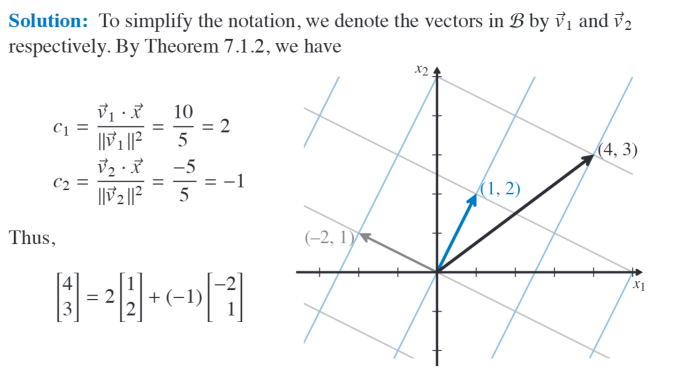
Finding $c_i$ of an orthogonal basis ? $c_i$ = $\frac{v \cdot x}{|v|^2}$
- If finding a linear combination, just apply for each basis vector
Orthonormal Sets
?
- Orthogonal set of vectors where each vector v is a unit vector
- $||v_1||$ = 1 for all 1 <= i <= k
Inverse/Transpose ?
- Inverse of matrix equals transpose when orthonormal set
- Columns and rows of P form orthonormal basis for $R^n$
- $P^T = P^{-1}$
Examples
Orthonormal Set
References:
Created:: 2022-03-26 19:12