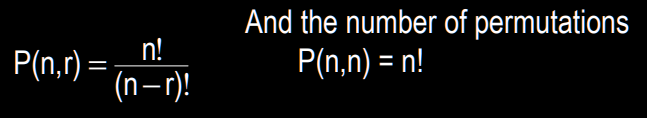Status: Tags: #archivedCards/macm101/combinatorics Links: Combinatorics
Permutations
Principles
Order matters in permutations
- ex) Position in a race
- ex) Giving positions of descending power (king, queen, jester, etc)
P(n,r) of permutations of size r from a collection of n objects can be found by ?
- Choosing r elements out of n, order matters
- n ways to choose first, n-1 to choose next
-
P(n) of permutations from a collection of n objects WITH REPEATED ELEMENTS can be found by
?
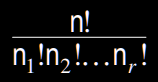
- $n_1$ … $n_r$ is the amount of repeated instances of an indistinguishable element
Examples
Slides
Example: In how many ways can we select 3 students from a group of 5 student to stand in a line for a picture? ? By the rule of product, there are 5 ⋅ 4 ⋅ 3 = 60 ways to select student
Example: How many permutations of the letters ABCDEFGH contain the string ABC? ? Because the letters ABC must occur as a block, we can find the answer by finding the number of permutations of six objects, namely, the block ABC and the individual letters D, E, F, G, and H. Since these six objects can occur in any order, there are P(6,6) = 6! = 720 options
Example:
How many different 4-letter words (not necessarily meaningful) can be built permuting the letters of the word COOL
?
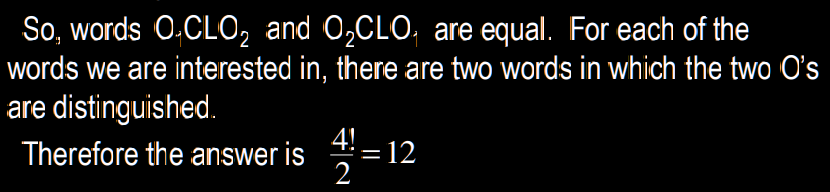
Example of repetition:
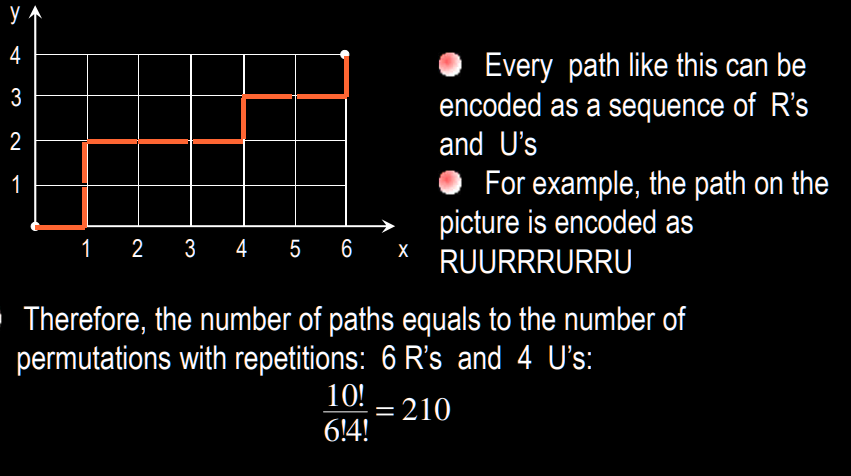
Determine the number of (staircase) paths in the xy-plane from (0,0) to (6,4), where each such path is made up of individual steps going one unit to the right (R) or one unit upward (U)
?
- If f(10,4), numerator is 4 largest while denom is 4 smallest
Assignment
A9Q2: There are five distinct computer science books, three distinct mathematics books, and two distinct art books. In how many ways can these books be arranged on a shelf if every two of the five computer science books are separated from each other by at least one other book? ? We choose an arrangement of this type as follows. First we arrange the 8 non-computer science books in a row, this can be done in 5! ways. Since the computer science books must not stand next to each other, there are 6 places for them: 1 before all the other books, 4 between them, and 1 after all the other books. If we number the two computer science books in some way, then the number of ways we can place them equals the number of permutations of size 5 out of 6 places. There are P(6, 5) of such ways, and by the rule of product 5! · P(6, 5) of possible arrangements
A9Q3:There are five distinct[A9Q3:There are five distinct computer science books, three distinct mathematics books, and two distinct art books. In how many ways can these books be arranged on a shelf if one of the art books is on the left of all the mathematics books, and the other art book is on the right of all the mathematics books? ](a9q3:There are five distinct computer science books, three distinct mathematics books, and two distinct art books. In how many ways can these books be arranged on a shelf if one of the art books is on the left of all the mathematics books, and the other art book is on the right of all the mathematics books?) computer science books, three distinct mathematics books, and two distinct art books. In how many ways can these books be arranged on a shelf if one of the art books is on the left of all the mathematics books, and the other art book is on the right of all the mathematics books? ? We split selecting an arrangement for these 10 books as follows. First, we place the 3 mathematics books in a certain order (there are 3! ways to do that). Second, we place one art book before the mathematics ones, and one after them (there are 2 ways to do this). Next, we are going to place the five computer science books into the remaining 6 positions. However, some of the computer science books can stand next to each other, therefore we further divide this process into five stages. First, we place the first computer science book, there are 6 ways to do that; then we place the second computer science book, then the third one, the fourth one, and the fifth one. There are 7, 8, 9, and 10 ways to do that. Finally by the rule of product, the total number of arrangements is the product of all the numbers above.
Backlinks
|
|
References:
Created:: 2021-11-04 08:44