Status: Tags: #archivedCards/macm101/combinatorics Links: Combinatorics
Pigeonhole Principle
?
- If m pigeons occupy n pigeonholes and m>n, then at least one pigeonhole has two or more pigeons roosting in it
Examples
- Among any group of 367 (or more) people, there must be at least two with the same birthday, because there are only 366 possible birthday
While on a four-week vacation, Herbert will play at least one set of tennis each day, but he will not play more than 40 sets total during this time. Prove that no matter how he distributes his sets during the four weeks, there is a span of consecutive days during which he will play exactly 15 sets.
?
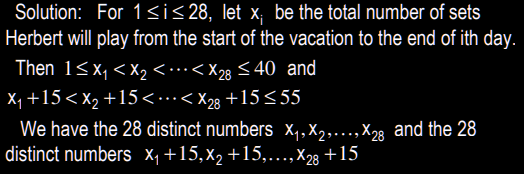
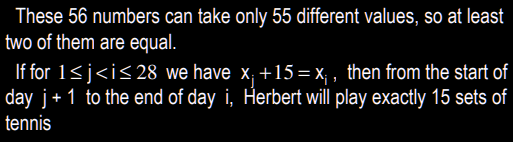
If n objects are placed into k boxes, then there is at least one box containing at least $\lceil \frac{n}{k} \rceil$ objects. ?
- Prove by contradiction
- Suppose boxes contain no more than $\lceil \frac{n}{k} \rceil - 1$ objects. Then, # objects is at most
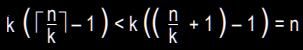
- The claim is that at least one of the k boxes contain at least ⌈N/k⌉ objects.
- The proof goes by contradiction: Suppose the claim is false, then each box must have strictly less than ⌈N/k⌉ objects, i.e., at most ⌈N/k⌉−1 objects (the greatest integer strictly less than n is n−1)
Assume that in a group of six people, each two individuals are either friends or enemies. Show that there are either three mutual friends or three mutual enemies in the group. ?
- Let A be one of the six people
- Of the five other people in the group, there are either three or more who are friends of A, or three or more who are enemies of A. Indeed, by the generalized pigeonhole principle, when 5 objects are divided into 2 sets, one of the sets contains at least $\lceil \frac{5}{2} \rceil = 3$ objects.
- In the former case, suppose that B, C, and D are friends of A. If any of these 3 individuals are friends, then these two and A form a group of 3 friends.
- Otherwise, B, C, and D form a group of 3 enemies
Backlinks
|
|
References:
Created:: 2021-11-15 11:19