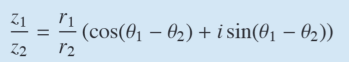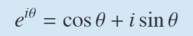Status: Tags: #cards/math232/unit9 Links: Complex Numbers
Polar Forms
Principles
Polar representation of complex numbers
?
Polar form of a complex number z is ?
- $z = r(cos\theta + isin\theta)$
- r = |z| and theta is an arg of z
In polar form, z1z2 = ?
- $r_1r_2(cos(\theta_1+\theta_2) + isin(\theta_1+\theta_2))$
In polar form, z1/z1 =
?
How to turn complex number into euler form and the principal argument ?
- Find $r$ which is the length of $z$
- find theta through $cos\theta = \frac{x}{r}$
- Plug into polar form $z = r(cos\theta + isin\theta)$
- To find principal argument, take calculated $\theta$ that is within range $-\pi <= x <= \pi$
How to turn euler form into complex number ?
- turn radian into theta, coefficient into r
- $z = r(cos\theta + isin\theta)$
- solve cos and sin using unit circle
- distribute coefficient
Euler’s Formula
?
- Allows us to write $z=re^{i\theta}$
- and $z^n=r^ne^{in\theta}$
References:
Created:: 2022-03-09 15:47