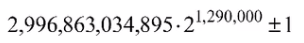Last updated Unknown

Status: Tags: #archivedCards/macm101/numbertheory Links: Number Theory

Prime Numbers

Every integer n (except for 1 and -1) has at least 2 positive divisors, 1 and n itself (or -n). A positive number that does not have another positive divisor is called prime. Non-prime numbers are called Composite Numbers

Principles

Division

• If a,b are integers and p is prime such that p | ab then p | a or p | b
• If $a_i$ is an integer for 1<=i<=n, p is prime and p | a_1,a_2, etc, then p | $a_i$ for some 1<=i<=n
• Fundamental Theorem of Arithmetic

Types

Mersenne numbers

• Form $M_n = 2^n - 1$

Relative primes ? When gcd between two numbers is 1

Theorems

How many prime numbers are there? ?

• Euclid’s theorem, there are infinitely many prime numbers
• 

Open Problems

• Goldbach’s conjecture
  • Every positive even number can be represented as the sum of two prime numbers.
  • For example: 4 = 2 + 2, 8 = 5 + 3, 42 = 37 + 5
  • Goldbach’s conjecture is known to be true for even numbers up to $4(10)^18$
• Twin prime conjecture
  • Twin primes are primes that differ by 2, such as 3 and 5, 5 and 7, 11 and 13, etc. The Twin Prime Conjecture asserts that there are infinitely many twin primes. The record twin primes:

Backlinks

1

list from Prime Numbers AND !outgoing(Prime Numbers)

References:

Created:: 2021-11-25 15:55