Last updated April 10, 2022

Status: Tags: #archivedCards/macm101/numbertheory Links: Residues

Residues

• Residue of an integer a modulo m is such a number b that a = b (mod m ) and 0 <= b < m
  • Remainder of a when divided by m

Operations on Residues Set

Can create set of residues, denote as $Z_m$

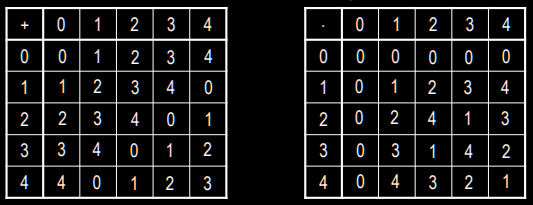
• a + b (mod m) is the element c ∈ $Z_m$ such that c ≡ a + b (mod m)
• a – b (mod m) is the element c ∈ $Z_m$ such that c ≡ a – b (mod m)
• a ⋅ b (mod m) is the element c ∈ $Z_m$ such that c ≡ a ⋅ b (mod m)
• Stays as element in residue set

Construct + and x operation table for $Z_5$

Types

Inverse Residues

?

Proving

Prove 3 mod 7 ?

Proper Divisors

Proper divisor of 0 ?

• A proper divisor of 0 modulo m is a residue a such that there is b ≡ 0 (mod m) with a ⋅ b ≡ 0 (mod m). has a proper divisor of zero. does not.

Backlinks

1

list from Residues AND !outgoing(Residues)

References:

Created:: 2021-12-02 15:19