Last updated April 10, 2022

Status: Tags: #cards/cmpt225/dataStructures/trees Links: Binary Search Trees

Self-balancing/AVL BST

Principles

?

• A BST in which the height of its left subtree and the height of its right subtree differ by at most 1

AVL tree ?

• Worst case scenario of insertion, deletion, search is O($log_2$n)
• Adelson-Velskii and Landis invited in 1962
• balancing property

AVL tree rotation steps ?

• Is the tree a BST?
• Which node is out of balance?
  • start considering nodes at level H - 1 and ascertain whether or not they are balanced nodes, i.e., their subtrees have heights differing by at most 1
  • We can skip nodes at level H - Why?
  • We work our way up to the root, until we find the node that is out of balance
  • From this out of balance node, we apply the AVL 9 balancing algorithm
• What rotation should be applied to rebalance?
• Apply rebalance
• Is tree now AVL?
  • Start at insertion and work way up
    • Declared unbalanced or balanced if at root
    • Other side should be balanced
• Is tree still BST?

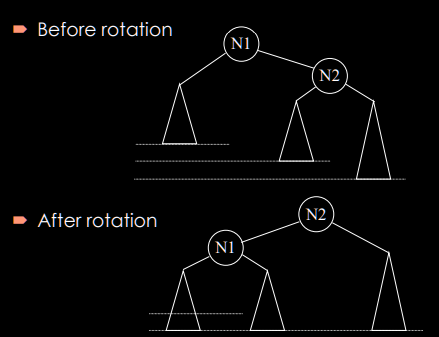
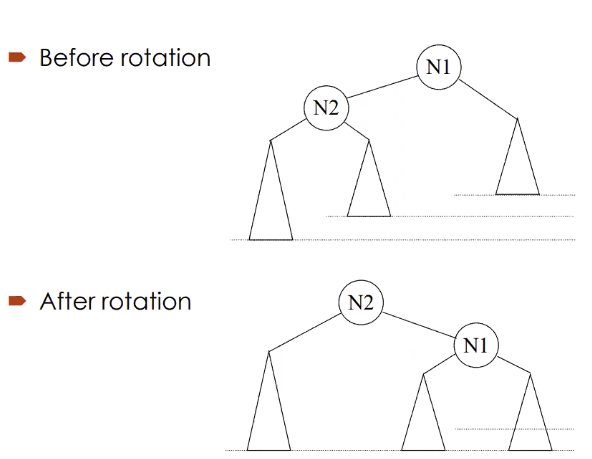
Rotations

• 1st letter is which side is taller, 2nd letter is subtree

Single/Outside Rotations

• Case 1: RR rotation
  • 
• Case 2: LL rotation
  • 

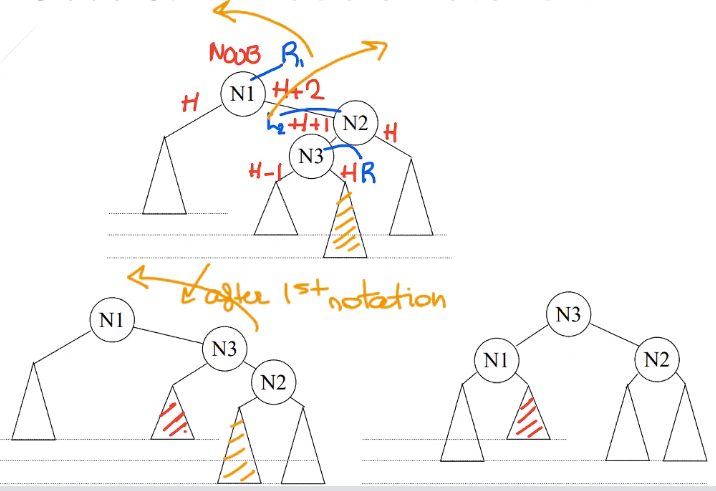
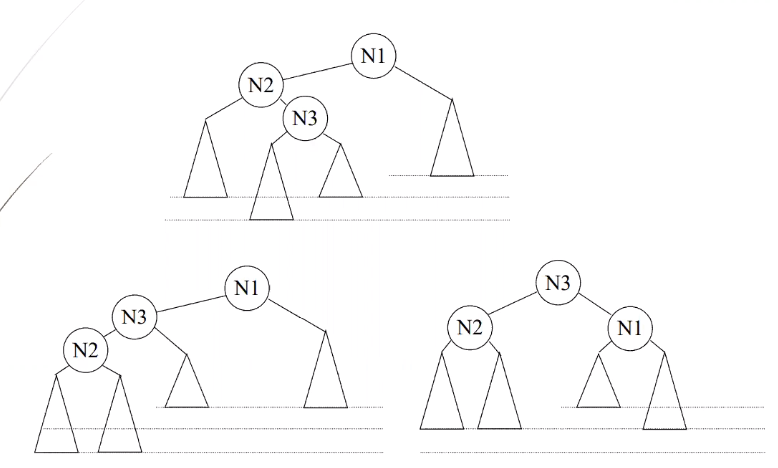
Double/Internal Rotation

• Case 3: RL rotation
  • 
  • First move, 3 goes in between n1 and n2
    • n3→right goes to n2→left
    • n3→right becomes n2
    • n1→right becomes n3
  • Second move, n3 becomes root
    • n3→left = n1
• Case 4: LR rotation
  • 
  • First move, 3 goes in between n1 and n2
    • n3→left goes to n2→right
    • n3→left becomes n2
    • n1→left becomes n3
  • Second move, n3 becomes root
    • n3→right = n1

How to self-balance ?

• Rotation (4 possible types)

Time Efficiency

insert, remove, retrieve ;; O(logn) successor ;; O(logn) min/max ;; O(logn)

References:

Created:: 2022-02-28 16:11