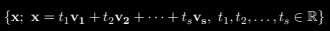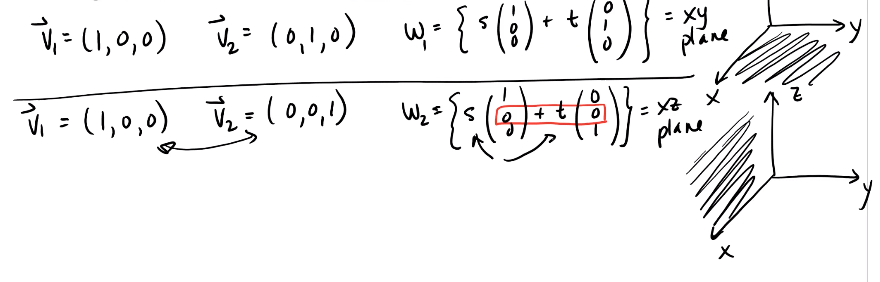Status: Tags: #cards/math232/unit1 Links: Vectors
Span
Principles
Span of vectors $v_1$, $v_2$, $v_3$ … $v_s$ ?
- the set of all linear combinations of the vectors
-
- Denoted by span{vectors}
Determining span
Determining span for $R^2$ of 2 points
- See if you can travel to any point of the plane using some $c_i$($p_i$) for all points
- Find the parametric equation for x,y, etc
- Isolate one variable for both equqations
- set the equations equal to each other via the variable
- Isolate the other variable, and use it to find the second
When it is LI
- Plug 0’s into the scalar equation, if it = 0 then it is LI
Examples
What is the set W1 = span{e1, e2}, where e1, e2 are the standard basis vectors in R2? ?
- $R^2$
What is the set W2 = span{e1, e2, e3}, where e1, e2, e3 are the standard basis vectors in R3? ?
- $R^3$
What is the set W3 = span{(−1, 4)}? ?
- Since it’s just a line, it would just be -4x
What is the set W4 = span{(1, 0, 5),(0, 1, 5)}? ?
- 1st point is not a multiple of the 2nd, so span will be all linear combinations of (1 0 5) and (0 1 5), goes through origin
- t(1 0 5) + s(0 1 5)
Suppose v1 and v2 are vectors in R3. Consider the set W = span{v1, v2} = {sv1 + tv2; s,t ∈ R} Investigate the set W for different vectors v1 and v2 ?
-
- If both points only have x, y, or z values, then it will just be a line
Backlinks
References:
Created:: 2022-01-11 20:00