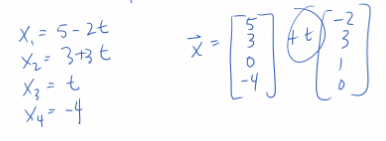Status: Tags: #cards/math232/unit2 Links: Vector Line Equations
System of linear equations
Principles
?
- Every linear system can have how many solutions ;; 0,1,infinity
To vector form
- Multiply c scalars into vector, then turn into RREF
Types
Solution Sets
- 2 equations of planes (x,y,z)
- Solution set is a line if they intersect
Solving
Steps ?
- Convert into Augmented Matrix
- Row operations
- RREF
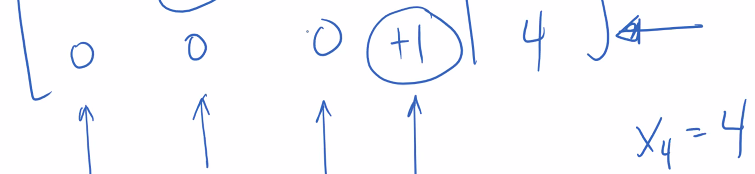
- Identify leading variables (pivot columns)
- Identify Free variables
- Write out solution set (infinite if 1+ free)
Various linear systems can have the same solution set, the goal of solving is by finding a more simpler matrix that we can easily find the solution of
- Even to the point where one of the variables is simply isolated
- Can be simplified using an Augmented Matrix
We can manipulate the given linear system one of three ways:
- Multiply one of equations by a non-zero scalar
- Interchange two equations
- Add a multiple of one equation to another
- in 2x2, goal is to have 1 on diagonal, 0 bottom left to isolate $x_2$
- Gaussian elimination, make 0s under 1
- If a column has no appropriate 1 upon finding a solution, then it is a parameter
- After isolating one, you slowly go up the chain and substitute and convert into a line
- For a specific one, just set t equal to something and prove the point
Backlinks
|
|
References:
Created:: 2022-01-19 18:03