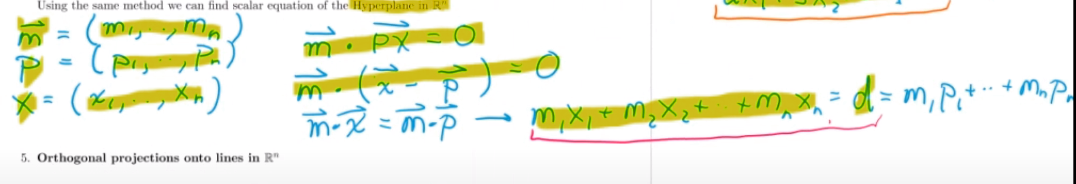Last updated Unknown

Status: Tags: #cards/math232/unit1 Links: Vectors

Vector Plane

$R^3$

Principles

• ?
• $v_1$ determines location on the plane
• $v_2$ and $v_3$ are free since they must be an $R^2$ span

• Requires orientation (tilt, normal direction, perpendicular to surface)
  • Position in space is based on p
  • q is on plane if n(PQ) = 0, can be turned into nq = np
    • where PQ = q-p
    • becomes $ax_1$ + $bx_2$ + $cx_3$ = d = $ap_1$ + $bp_2$ + $cp_3$
      • $ax_1$ + $bx_2$ + $cx_3$ = d is Scalar equation of plane

$R^n$

Procedures

• Finding angle between two planes

Check if a vector is in a plane ?

• Plug vector components into plane variables, check if = 0

Backlinks

1

list from Vector Plane AND !outgoing(Vector Plane)

References:

Created:: 2022-01-19 00:15