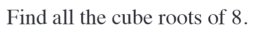Status: Tags: Links: Complex Numbers
n-th Roots
Principles
Using Moivre’s formula for n-th powers to find n-th roots ?
- We need to find Complex Numbers $z=re^{i\theta}$, a number w such that $w^n=z$. Suppose $w=Re^{io}, then $w^n=z$ implies that
-
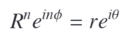
- R is real n-th root of pos real number r. But since its restricted only to addition of 2pik, then we can only say
-
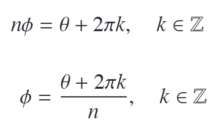
If $z = re^{i\theta}$ is non-zero, then the n distinct n-th roots of z are
?

Examples
- Continuing just leads to the key roots
Find fourth roots of -81 and illustrate in an Argand diagram
?
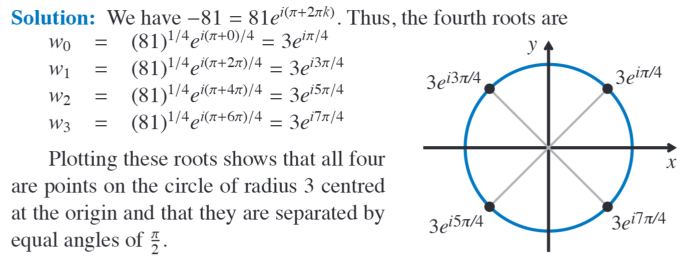
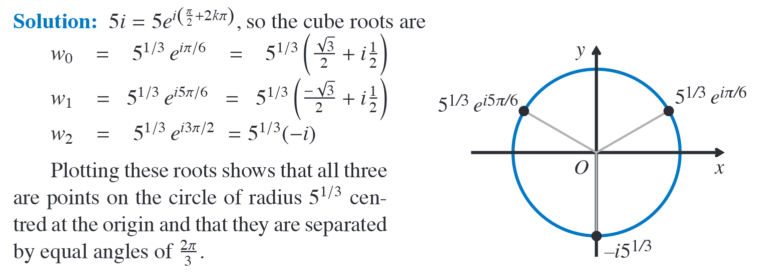
Find third roots of 5i and illustrate in an Argand diagram
?
References:
Created:: 2022-03-08 19:34