Property of tree: unique path from root node to any other node
Max height of a tree with n nodes is ;; n-1
Minimum height of a tree with n nodes is ;; floor(log2n)
Number of nodes in a h tall binary tree can range from ;; h to 2h−1
Nodes
Height of a node v
?
Length of longest path from node v to a leaf
Level of a node v
?
Root is 1, down from there
Depth
?
length of path from v to root
Degree of a node
?
Number of edges that touch a node v
Internal has deg > 1
External node = 1 or < 1
Types
Full tree
?
All nodes at level < h have max number of children
Complete tree
?
Full all way to h-1 with level h filled in from left to right without any gap
Can only be far left with H nodes but would be complete since no gap
Balanced tree
?
N-ary tree with all n subtrees of any nodes have height that differ by at most 1
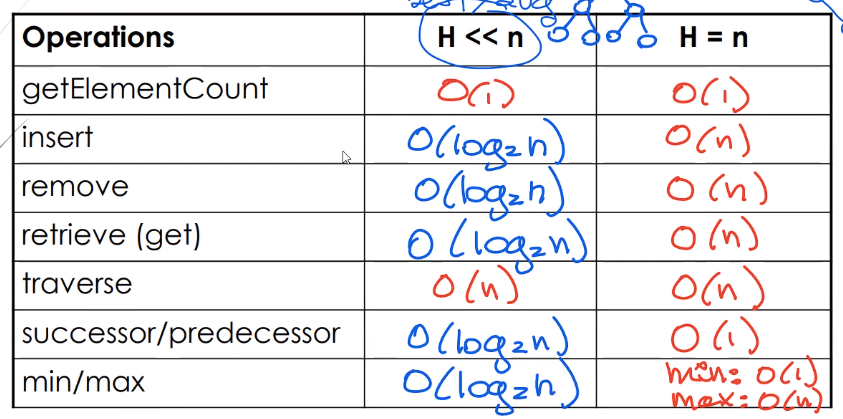
Operations
Overview
1
2
3
4
5
6
7
8
9
10
set_left_child(BTnode_t* parent, BTnode_t* left_child): set a node to be the left child of another node
set_right_child(BTnode_t* parent, BTnode_t* right_child): : set a node to be the right child of another node
is_leaf(BTnode_t* root): check if a node is leaf or not
size(BTnode_t* root): returns the number of nodes in the tree
height(BTnode_t* root): returns the height/depth of the tree
print_pre_order(BTnode_t* root): traverses the tree in pre-order way and prints the nodes
print_in_order(BTnode_t* root): traverses the tree in in-order way and prints the nodes
print_post_order(BTnode_t* root): : traverses the tree in post-order way and prints the nodes
count_leaves(BTnode_t* root): Counts the number of leaves in the tree • in_order_to_array(BTnode_t* root): Puts all elements of tree in an array with in-order traversal • are_equal(BTnode_t* root1, BTnode_t* root2): Checks if two nodes of the tree are equal(value and children) • BTnode_t* reconstruct_tree(int* inorder, int* preorder, int n): Reconstructs a tree given the number of nodes, the inorder traversal and the preorder traversal
InsertR
Examples
Implementation
struct BTnode {
int data; //struct BTnode* left; // left child
struct BTnode* right; // right child
struct BTnode* parent;
}
typedef struct BTnode BTnode_t;
struct binary_tree {
struct BTnode* root;
}
Inserting
1
2
3
4
5
6
7
8
if binary search tree empty
insert new element in root
otherwise
if new element < element stored in root
insert new element into left subtree
else
insert new element into right subtree
Let’s not forget to elementCount++
Retrieving
1
2
3
4
5
6
7
8
9
if binary search tree empty
target element not there!
if target element == element stored in root
return element stored in root
otherwise
if target element < element stored in root
search left subtree
else
search right subtree
